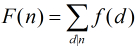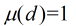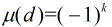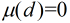莫比乌斯反演-白红宇

莫比乌斯反演

阅读量：6958 次

发布时间：2019-06-27

本文共 2410 字，大约阅读时间需要 8 分钟。

莫比乌斯反演

当满足以下求和函数：

可以得到：

F(1)=f(1) F(2)=f(1)+f(2)

F(3)=f(1)+ f(3) F(4)=f(1)+f(2)+f(4) F(5)=f(1)+f(5)

推出：

f(1)=F(1) f(2)=F(2)-f(1)=F(2)-F(1)

f(3) =F(3)-F(1) f(4)=F(4) -f(2)- f(1) =F(4)-F(2)

f(5) =F(5)-F(1)

可以反推出求f（x）的式子：

在上面的公式中有一个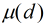函数，它的定义如下：

（1）若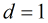，那么

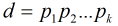
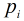
（2）若，均为互异素数，那么

（3）其它情况下

而函数可以通过筛选求出：

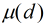
然后是关于莫比乌斯求GCD的原理，当时看了很久感觉并无法满足上面公式，后来才发现还有公式2(╯▽╰)

即F[n]等于n的倍数d,f[d]的和，然后可以反演出后面公式

对于GCD（x，y） = k

设f[d]： GCD(x,y) = k ，即最大公约数为k的（x，y）的对数

F[n]： n|GCD（x，y），即最大公约数是n的倍数的（x，y）的对数

所以：F{1] = f[1] + .... + f[n]

F[2] = f[2] + f[4] + ....f[2*i]...

可以发现完全满足上面的公式

而且对于F[n]，可以求出F[n] = （a/n）*（b/n）

因此我们可以再利用反演求f[d]

void Moblus(){    tot = 0;    memset(is_prime,0,sizeof(is_prime));    mu[1] = 1;    for(int i = 2; i <= maxn; i++)    {        if(!is_prime[i])        {            prime[tot++] = i;            mu[i] = -1;        }        for(int j = 0; j < tot; j++)        {            if(prime[j]*i>maxn)                break;            is_prime[i*prime[j]] = 1;            if(i % prime[j])             //prime[j]不重复            {                mu[i*prime[j]] = -mu[i];            }            else            {                mu[i*prime[j]] = 0;                break;            }        }    }}

题：，

关于优化：

在计算中，我们是枚举1->n计算，每次ans+= mu[i] * (a/i) * (a/i)

我们可以发现，由于是除法计算，所以经常出现a/i = a/(i+1) = .... = a/(i+k) 例如：8/3 = 8/4

所以每次循环我们可以计算出，相等值的长度，然后在用sum保存mu的和，一次循环便能计算出一段数的值

ll gett(int n,int m)        //分块优化  {      ll ret = 0;      int i,last;      if(n > m)          swap(n,m);      for(i = 1,last = 0;i<=n;i=last+1)      {           last = Min(n/(n/i),m/(m/i));      //求为n/i时的最远位置           ret += (ll)(n/i)*(m/i)*(sum[last]-sum[i-1]);      }     return ret;  }

参考文章：

/************************************************分界线*******************************************************/

①：求GCD /*个人理解

对于求GCD，我们可以看成先求出所有选择的情况，然后减去GCD不为1（即把数分成各个因子的集合）

例：num[2]能被2约去的数，然后减去这些数，我们会发现减去了2,3后，6会被多减，所有需要加上，于是满足了

莫比乌斯函数.大致思路：

C(n,k) － C(gcd只含奇数个质数的个数,k) ＋ C(gcd只含偶数个质数的个数,k)，前面的符号就是莫比乌斯函数

一种是求1≤x≤n，1≤y≤m中多少对(x,y)满足gcd(x,y) = 1, /*比如上面的hdu1695

推出公式：for(i->min(n,m)) ans += mu[i]*(n/i)*(m/i),

完全可以看成在i = 1时求出所有情况，然后2的倍数（即可能gcd = 2的情况），减去3的倍数...加上6的倍数......。

另一种是给你特定的几个数，让你求他们互质的情况（其中k个数互质）。

我们也是先计算出总的情况，而且筛选出，每个这些数中，是i的倍数的个数，用num保存。